Abstract
How effective are push promotions through mobile apps for brick-and-mortar retailers and what strategies can improve the performance of targeted push marketing? To address these questions, we develop a multivariate event history model to evaluate the effects of behavior and location-based push promotions on shoppers’ app usage and offline shopping activities. Our study generates new insights into mobile app promotions and offline shopping. We find that behavior-based pushes have a higher impact on consumer responses before a shopping trip than during a trip, and their effects vary significantly across different types of retailers. The effects of pushes are positively correlated with shoppers’ propensities of app pulls and mall visits, which suggests that timing the delivery of pushes can make them more effective. Furthermore, location-based pushes exhibit stronger positive effects on app pulls and coupon outclicks during a shopping trip than behavior-based pushes, even after shoppers receive the latter before the trip, which shows that behavior and location-based pushes are not substitutable. We demonstrate through simulations that our model enables marketers to design more effective mobile targeting strategies by exploiting heterogeneous consumer responses. Addressing potential endogeneity by controlling for the information used for customer selection in the customer’s response functions, our proposed model can be applied to many empirical problems involving event history data.







Similar content being viewed by others
Notes
According to the publisher, these app users account for about 50% of their total user base in the city who share locations and receive pushes.
The publisher’s experiments with mobile phones and the app show that whether a phone is in a pocket or a purse or in the shopper’s hand, the direction of a shopper’s movement and certain blind spots inside a mall may cause weaker signal strength and failure of delivery of the message.
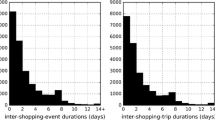
Discretizing the events into the daily level is only used for exploratory analysis to provide model-free evidence. Our model is continuous-time and accounts for the exact timing of each event.
Our exploratory data analysis finds that the daily number of mall visits is positively influenced by the number of app pulls before mall visits. However, the number of mall visits does not have a significant effect on the number of the app pulls on the following day (\(p=0.916\)). We also test the difference between the number of app pulls before and after a mall visit in a day and find no statistically significant difference (\(p=0.781\)). Hence, we conclude that the correlation between mall visits and app pulls is attributed to the effect of app pulls on mall visits.
Indeed, two events do not occur at the exact same time in our data.
The intensity function \(\lambda _{k}^{i}(t|H_{t}^{i})\), depending on the entire history of past events, the inter-event time intervals and time elapsed since the previous event, is a generalization of the hazard function. If \(\lambda _{k}^{i}(t|H_{t}^{i})\) only depends on the time of the immediate previous event in the history \(H_{t}^{i}\), it is a hazard function. Please refer to Aalen et al. (2008) for technical details.
The decision to opt for the log specification is driven by the highly right-skewed distribution of coupon outclicks and a significant percentage of zero outclicks. Moreover, our belief is that the effect of coupon outclicks should exhibit concavity, implying that a large number of outclicks will not yield an outsized effect, as would be the case in a linear functional form.
To determine whether a geometric (exponential) decay function is good choice in our model, we have fitted different versions of our model using the following decay functions: 1). the Gaussian decay function \(\exp \left( -\rho t^{2}\right) \), 2). the inverse decay function \(1/\left( 1+\rho t\right) \) and 3). a Matérn-kernel type of decay \((1+\rho t)\exp \left( -\rho t\right) \), where the modified Bessel function \(K_{\nu }\)’s v parameter is equal to 3/2. We compare the model fit of different versions of our model with different decay functions using the Bayes factor (marginal likelihood). We find that the model with the exponential decay actually has the highest marginal likelihood and hence the best fit among these models.
We have also tested the model \(Poisson\left( \vartheta _{k}^{i}exp\left\{ \vartheta _{k1}\sum _{t'<t}W_{t',1}^{i}g(t-t';\phi _{0k})\right\} \right) ,k=1,2\) for outclicks inside and outside mall. The parameter estimates of \(\vartheta _{k1}\), which is the direct effect of previous pushes on outclicks, are not significant in both models. Hence, the direct push effects are not included in the final model for outclicks.
We thank an anonymous reivewer for this suggsetion to categorize potential endogeniety concerns.
Due to our nondisclosure agreement with the publisher, we are unable to reveal the exact formula used by them for calculating these affinity scores.
We have also tested the same functions of \(S_{t}^{i}\) in the model for the app pulls inside malls during a mall visit but we find none of the coefficients in \(q(S_{t}^{i},\eta _{3}^{i})\) is significant.
We thank the Editor who suggested this approach to address the endogeneity issue in this model.
To conserve space and limit the length of our paper, we only report the means of the heterogeneous parameters in the main text and provide the standard deviations of the the heterogeneous parameters in Appendix E. Our results show substantial heterogeneity in most parameters, which will help improve the performance from customer target selection in Section 6.
The publisher mentioned to us that there is usually a time lag of several days between the time when the publisher selects the promotion recipients and when the push message is sent. This delay is because it is the publisher’s business practice to notify the retailer how many and which customers will receive the promotion in advance. However, which exact date of the affinity scores is used in the selection for each push is not recorded in our data.
References
Aalen, O. O., Borgan, O., & Gjessing, H. K. (2008). Survival and Event History Analysis: A Process Point of View. Springer.
Aghajanian, S. (2022). Mobile push notifications: An absolute necessity for mobile app marketing. https://vwo.com/blog/mobile-push-notifications/
Andrews, M., Luo, X., Fang, Z., & Ghose, A. (2016). Mobile ad effectiveness: Hyper-contextual targeting with crowdedness. Marketing Science, 35(2), 218–233.
Bernritter, S. F., Ketelaar, P. E., & Sotgiu, F. (2021). Behaviorally targeted location-based mobile marketing. Journal of the Academy of Marketing Science, 49(4), 677–702.
Braun, M., & Moe, W. W. (2013). Online display advertising: Modeling the effects of multiple creatives and individual impression histories. Marketing Science, 32(5), 753–767.
Danaher, P. J., Danaher, T. S., Smith, M. S., & Loaiza-Maya, R. (2020). Advertising effectiveness for multiple retailer-brands in a multimedia and multichannel environment. Journal of Marketing Research, 57(3), 445–467.
Danaher, P. J., Smith, M. S., Ranasinghe, K., & Danaher, T. S. (2015). Where, when and how long: Factors that influence the redemption of mobile phone coupons. Journal of Marketing Research, 52(5), 710–725.
Deshdeep, N. (2022). Mobile app or website? 10 reasons why apps are better. https://vwo.com/blog/10-reasons-mobile-apps-are-better/.
eMarketer (2019). US time spent with mobile 2019. https://www.insiderintelligence.com/content/us-time-spent-with-mobile-2019
Fong, N., Zhang, Y., Luo, X., & Wang, X. (2019). Targeted promotions on an e-book platform: Crowding out, heterogeneity, and opportunity costs. Journal of Marketing Research, 56(2), 310–323.
Fong, N. M., Fang, Z., & Luo, X. (2015). Geo-conquesting: Competitive locational targeting of mobile promotions. Journal of Marketing Research, 52(5), 726–735.
Gabry, J., Simpson, D., Vehtari, A., Betancourt, M., & Gelman, A. (2019). Visualization in Bayesian workflow. Journal of the Royal Statistical Society: Series A (Statistics in Society), 182(2), 389–402.
Gamba, A. (2021). 3 reasons why mobile apps are the future of your retail destination. https://www.coniq.com/resources/3-reasons-why-mobile-apps-are-the-future-of-your-retail-destination/
Ghose, A., Li, B., & Liu, S. (2019). Mobile targeting using customer trajectory patterns. Management Science, 65(11), 5027–5049.
Goldsmith, K., & Amir, O. (2010). Can uncertainty improve promotions? Journal of Marketing Research, 47(6), 1070–1077.
Hernández-Orallo, J., Flach, P., & Ferri Ramírez, C. (2012). A unified view of performance metrics: Translating threshold choice into expected classification loss. Journal of Machine Learning Research, 13, 2813–2869.
Kalbfleisch, J. D., & Prentice, R. L. (2002). The Statistical Analysis of Failure Time. John Wiley & Sons.
Kim, M., Bradlow, E. T., & Iyengar, R. (2022). Selecting data granularity and model specification using the scaled power likelihood with multiple weights. Marketing Science, 41(4), 848–866.
Kivetz, R., & Zheng, Y. (2017). The effects of promotions on hedonic versus utilitarian purchases. Journal of Consumer Psychology, 27(1), 59–68.
Knorex (2020). Why is mobile advertising effective? https://www.knorex.com/blog/articles/why-is-mobile-advertising-effective
Koch, L. (2019). Two-thirds of shoppers check phones in-store for product information, skipping store associates. https://www.insiderintelligence.com/content/two-thirds-of-internet-users-check-phones-in-store-for-product-information-skipping-store-associates
Li, C., Luo, X., Zhang, C., & Wang, X. (2017). Sunny, rainy, and cloudy with a chance of mobile promotion effectiveness. Marketing Science, 36(5), 762–779.
Li, H. A., & Kannan, P. (2014). Attributing conversions in a multichannel online marketing environment: An empirical model and a field experiment. Journal of Marketing Research, 51(1), 40–56.
Luo, X., Andrews, M., Fang, Z., & Phang, C. (2014). Mobile targeting. Management Science, 60(7), 1738–1756.
Lycka, K. (2017). How push notifications can influence traffic and revenue for an online shop [case study]. https://www.asymbo.com/how-push-notifications-can-influence-traffic-and-revenue-for-an-online-shop-case-study/
Marhamat, B. (2021). Shoppers still value in-store retail experiences. https://www.forbes.com/sites/forbesbusinessdevelopmentcouncil/2021/11/22/shoppers-still-value-in-store-retail-experiences/?sh=18ef28994fb3
Mocaplatform.com (2017). Transforming shopping mall experience leveraging mobile location technology. https://www.mocaplatform.com/blog/transforming-shopping-mall-experience-leveraging-mobile-location-technology
MoEngage (2021). Push notifications CTR, success rate and metrics for 2021. https://www.moengage.com/learn/push-notifications-ctr-success-rate-and-metri cs/
Narang, U., & Shankar, V. (2019). Mobile app introduction and online and offline purchases and product returns. Marketing Science, 38(5), 756–772.
OneSignal.com (2020). Outcomes: Push notification insights that go beyond CTR. https://onesignal.com/blog/push-notification-insights-that-go-beyond-ctr/
Park, C. H., & Park, Y.-H. (2016). Investigating purchase conversion by uncovering online visit patterns. Marketing Science, 35(6), 894–914.
PushEngage (2022). Push notification vs sms: Which one is more effective? https://www.pushengage.com/push-notification-vs-sms/
Retail Leader (2018). Macy’s develops new in-store experience. https://retailleader.com/macys-develops-new-store-experience
Statista.com (2021). Reactions of smartphone users in the united states when receiving too many push notifications from mobile apps as of june 2021. https://www.statista.com/statistics/1242709/us-too-many-push-notifications-users-reaction/
Stocchi, L., Pourazad, N., Michaelidou, N., Tanusondjaja, A., & Harrigan, P. (2021). Marketing research on mobile apps: past, present and future. Journal of the Academy of Marketing Science, (pp. 1–31).
Vanvani, S. (2022). The importance of mobile app marketing in today’s era; how brands are leveraging technology to draw consumers? https://timesofindia.indiatimes.com/blogs/voices/the-importance-of-mobile-app-marketing-in-todays-era-how-brands-are-leveraging-technology-to-draw-consumers/
Xu, L., Duan, J. A., & Whinston, A. (2015). Path to purchase: A mutually exciting point process model for online advertising and conversion. Management Science, 60(6), 1392–1412.
Zantedeschi, D., Feit, E. M., & Bradlow, E. T. (2017). Measuring multichannel advertising response. Management Science, 63(8), 2706–2728.
Zhang, J. Z., Netzer, O., & Ansari, A. (2014). Dynamic targeted pricing in B2B relationships. Marketing Science, 33(3), 317–337.
Zhang, Q. & Zhou, M. (2018). Nonparametric bayesian lomax delegate racing for survival analysis with competing risks. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R. Garnett (Eds.), Advances in Neural Information Processing Systems, volume 31: Curran Associates, Inc.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declared no potential conflicts of interest that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is based on part of the first author’s dissertation at the Univeristy of Texas at Austin. The authors would like to thank the company, which wishes to remain anonymous, that provided the data used in this study. The authors are grateful to the MSI Clayton Dissertation Award and seminar participants at Univerisity of Minnesota, Univeristy of Texas at Dallas, Emory University, Darthmouth College, Baruch College, Chinese University of Hong Kong, Tsinghua University and Fudan University for their constructive comments. The authors dedicate this article to their late friend, colleague, and coauthor, Frenkel ter Hofstede.
Appendices
Appendix A. MCMC algorithm
We derive from the variance-covariance matrix \(\Psi \) the correlation coefficient \(\rho =\Psi _{12}\Psi _{11}^{-\frac{1}{2}}\) and variance \(\sigma _{\mu }^{2}=\Psi _{11}\).
The following steps show the details of the MCMC algorithm used in this study:
Step 1: Sample \(\alpha ^{i}\). We consider the prior distribution of \(\alpha ^{i}\) following \(MVN_{4}(\theta _{\alpha }, \Sigma _{\alpha })\). We use the Metropolis-Hastings algorithm to sample \(\alpha ^{i}\). The accepting probability of the proposed \(\alpha ^{i*}\), drawn from a \(MVN_{4}\) distribution, is given as
Step 2: Sample \(\gamma ^{i}\). We consider the prior distribution of \(\gamma ^{i}\) following \(MVN_{14}(\theta _{\gamma }, \Sigma _{\gamma })\). We use the Metropolis-Hastings algorithm to sample \(\gamma ^{i}\). The accepting probability of the proposed \(\gamma ^{i*}\), drawn from a \(MVN_{14}\) distribution, is given as
Step 3: Sample \(\phi \). We consider the prior distribution of \(\phi _{j}\) following \(inverse-Gamma(\bar{a}_{\phi },\bar{b}_{\phi })\). We use the Metropolis-Hastings algorithm to sample \(\phi _{j}\). The accepting probability of the proposed \(\phi _{j}^{*}\), drawn from a log-normal distribution, is given as
Step 4: Sample \(\delta ^{i}\). We consider the prior distribution of \(\delta ^{i}\) following \(MVN_{3}(\theta _{\delta },\Sigma _{\delta })\). The accepting probability of the proposed \(\delta ^{i*}\), drawn from a \(MVN_{3}\) distribution, is given as
Step 5: Sample \(\pi ^{i}\). We consider the prior distribution of \(\pi ^{i}\) following \(MVN_{2}(\theta _{\pi }, \Sigma _{\pi })\). The accepting probability of the proposed \(\pi ^{i*}\), drawn from a \(MVN_{2}\) distribution, is given as
Step 6: Sample \(\vartheta ^{i}\). We consider the prior distribution of \(\vartheta ^{i}\) following \(log-MVN_{2}(\bar{\theta }_{\vartheta },\bar{\Sigma }_{\vartheta })\). The accepting probability of the proposed \(\vartheta ^{i*}\) drawn from an \(log-MVN_{2}\) distribution, is given as
Step 7: Sample \(\theta _{n}\). We consider the prior distribution of \(\theta _{n}\) following \(MVN_{Q}(\bar{\theta }_{\theta _{n}}, \bar{\Sigma }_{\theta _{n}})\), where \(\bar{\theta }_{\theta _{n}}=0\) and \(\bar{\Sigma }_{\theta _{n}}=10^{6}I_{Q}\). The next draw, \(\theta _{n}^{*}\), is drawn from a multivariate normal distribution
where \(M=N^{'}((\sum _{i=1}^{I}n^{i})^{'}\Sigma _{n}^{-1}+\bar{\theta }_{\theta _{n}}^{'}\bar{\Sigma }_{\theta _{n}}^{-1})^{'}\), \(N=(I\Sigma _{n}^{-1}+\bar{\Sigma }_{\theta _{n}}^{-1})^{-1}\) , \(n=\alpha ,\gamma ,\delta ,\pi ,\)and \(\vartheta \), and Q is the corresponding dimension of \(\theta _{n}^{*}\).
Step 8: Sample \(\Sigma _{n}\). We consider the prior distribution of \(\Sigma _{n}\) following \(IW(\bar{S}^{-1},\bar{\nu })\), where \(\bar{S}=I_{Q}\) and \(\bar{\nu }=1\). The next draw, \(\Sigma _{n}^{*}\), is drawn from an inverse Wishart distribution
where Q is the corresponding dimension of \(\theta _{n}^{*}\).
Appendix B. Addressing endogeneity of behavior-based push
To test the robustness of our results and whether our approach can sufficiently address the endogeneity issue, especially for the effects of behavior-based pushes, we have fitted three versions of our model with (a) the linear functions of \(S_{t}^{i}\), (b) the third-degree polynomials of \(S_{t}^{i}\), (c) a control function approach (using the linear functions of \(S_{t}^{i}\)), which assumes a probit model for the push selection \(W_{t,1}^{i}\in \{0,1\}\) and includes an additional random shock \(\varepsilon _{t}^{i}\) in the app pull intensity:
where j indexes the promotion category;\(X_{t,1}^{i}\) represents the weekend and holiday indicators; \(S_{t-3}^{i,r}\) is shopper \(i's\) affinity score for retailer r three days prior to the date of the push message. We assume that \(\varepsilon _{t}^{i}\) in (14) and \(v_{t}^{i}\) in (13) follow a joint bivariate normal distribution \(\left[ \varepsilon _{t}^{i},v_{t}^{i}\right] \sim N\left( 0,\Psi \right) \), where \(\Psi \) is a covariance matrix whose diagonal element (variance) for \(v_{t}^{i}\) is fixed at 1. The push selection modeled is jointly estimated using Bayesian inference with the models for app pulls, mall visits and coupon outclicks.Footnote 16 After fitting the models above, we find the correlation between \(\varepsilon _{t}^{i}\) and \(v_{t}^{i}\) is very small (the Bayesian posterior mean of the correlation in \(\Psi \) is 0.006 with the 95% posterior interval = (-0.015, 0.028)), which is consistent with the argument in Section 4.2 that flexibly controlling for \(S_{t}^{i}\) in the app pull and mall visit intensity functions indeed blocks the direct causal paths from \(S_{t-3}^{i,r}\) to the customers’ responses. Therefore, it is no longer necessary to apply the control function approach which uses \(S_{t-3}^{i,r}\) as an excluded variable. We have also fitted our model using a selected subsample of 2,375 customers (out of 5,000) whose affinity scores \(S_{t-3}^{i,r}\) are within a specified interval for each push promotion, ensuring overlap in the affinity scores between push recipients and non-recipients.
We obtained the following results for the parameters in our models. The table below shows that various forms of the flexible functions of \(S_{t}^{i}\) and the control function aproach yield very similar estimates, which demonstrates the robustness of our findings.
Appendix C. Posterior predictive checks and model comparison criterion
Based on the posterior estimates of the model parameters, we predict shoppers’ app pulls and mall visits in the 30 days following the estimation period. Following the recommendations in Gabry et al. (2019), we show in Fig. 1 the kernel density estimates of app pulls and mall visits in the holdout sample (the thick dark curve) vs. the predicated app pulls and mall visits (thin light curves), respectively, computed from 500 posterior draws of the parameter estimates. From the two plots in Fig. 1 it is evident that our proposed model fits the data very well.
We propose a metric based on the Brier score (Hernández-Orallo et al., 2012; Zhang and Zhou, 2018) to compare the models. Note that, for mall visits, we have
Hence, the cdf of the kth mall visit given the previous observations including the \((k-1)\)th mall visit is \(F_{N_{2}^{i}\left( t\right) }\left( t|H_{t}^{i}\right) =1-\exp \left( -\int _{t_{k}^{i}}^{t}\lambda \left( t|H_{t}^{i}\right) \right) dt\). After \(\lambda \left( t|H_{t}^{i}\right) \) is computed from the estimated parameters in the model, we calculate the modified Brier score as
where \(I\left( t_{k}^{i}|H_{t_{k}}^{i}\right) \) is an indicator function (empirical cdf ) which is equal to 1 for \(t\ge t_{k}^{i}\).
Appendix D. Simulation algorithm
Setup: K types of events, sequencially simulate points within the same day. No decay within a day.
-
1.
Draw parameters \(\alpha ^{i},\beta ^{i},\kappa ^{i},\gamma ^{i},\phi ^{i},\psi ^{i},\delta ^{i},\pi ^{i},\lambda _{p}^{i},\zeta ^{i},\omega ^{i}\) with replacement from the posterior samples.
-
2.
Simulate a point process in [0, T] given \(\alpha ^{i},\beta ^{i},\kappa ^{i},\gamma ^{i},\phi ^{i},\psi ^{i},\delta ^{i},\pi ^{i},\lambda _{p}^{i},\zeta ^{i},\omega ^{i}\),
-
1.
Divide [0,T] into daily intervals. At beginning of each day (t), compute \(\lambda _{t,k}^{i}=exp\{\delta ^{i}+\Pi _{t}^{i}X_{t}^{i}\!+\!\sum _{j=1}^{K}\sum _{t<t'}\alpha _{jk}^{i}g(t-t';\beta _{jk}^{i},\kappa _{jk}^{i})+\sum _{j=1}^{K}\sum _{t<t'}\gamma _{jk}^{i}Z_{jt}^{i}g(t-t';\phi _{jk}^{i},\psi _{jk}^{i})\}\) for \(k=1,2,\cdots ,K\).
-
2.
Simulate \(h\sim exp(\lambda _{t}^{i})\) where \(\lambda _{t}^{i}=\sum _{k}\lambda _{t,k}^{i},k=1,2,\cdots ,K\).
-
3.
If \(t+h<t'\) where \(t<t'<t+1\) is the time of a behavior-based push in the same day, simulate \(k\sim multinomial(p_{1},\cdots ,\,p_{K})\), where \(p_{k}=\frac{\lambda _{t,k}^{i}}{\lambda _{t}^{i}},k=1,2,\cdots ,K\). Keep the event k at \(t+h\). Reset t to \(t+h\). Repeat from (a).
-
4.
If \(t+h>t'\), reset t to \(t'\). Repeat from (a).
-
5.
If \(t+h>t+1\), reset t to \(t+1\), Repeat from (a).
-
6.
Continue until \(t>T\).
-
1.
-
7.
The simulation output is event times \(\{t_{1},\cdots ,t_{N}\}\) of event types \(\{k_{1,\cdots ,}k_{N}\}\).
Appendix E. Supplementary results
1.1 Means and variances of heterogeneous parameters in the model
1.2 Model estimates with half-day decaying effects
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, Z., Duan, J.A. & Mahajan, V. Push and pull: Modeling mobile app promotions and consumer responses. Quant Mark Econ (2024). https://doi.org/10.1007/s11129-024-09289-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11129-024-09289-w
Keywords
- Mobile app promotion
- Behavior-based push
- Location-based push
- Offline shopping
- Multivariate event history
- Counting process model